Probabilità avanzata, previsioni, probabilità e previsioni

Calcolo delle Probabilità Avanzato: Scopri i Segreti del Caso!

Ciao giovani matematici e detective del futuro, siete pronti a fare un salto nel mondo affascinante della probabilità avanzata? Non è solo tirare una moneta a testa o croce! Qui entriamo nel vivo di come le cose possono accadere, anche quando sembrano complicate!

Cosa vuol dire “Probabilità Avanzata”?

Immaginate di voler capire se domani pioverà o se la vostra squadra preferita vincerà la partita. La probabilità avanzata ci aiuta a fare previsioni più precise, anche quando gli eventi sono collegati tra loro o accadono uno dopo l’altro.

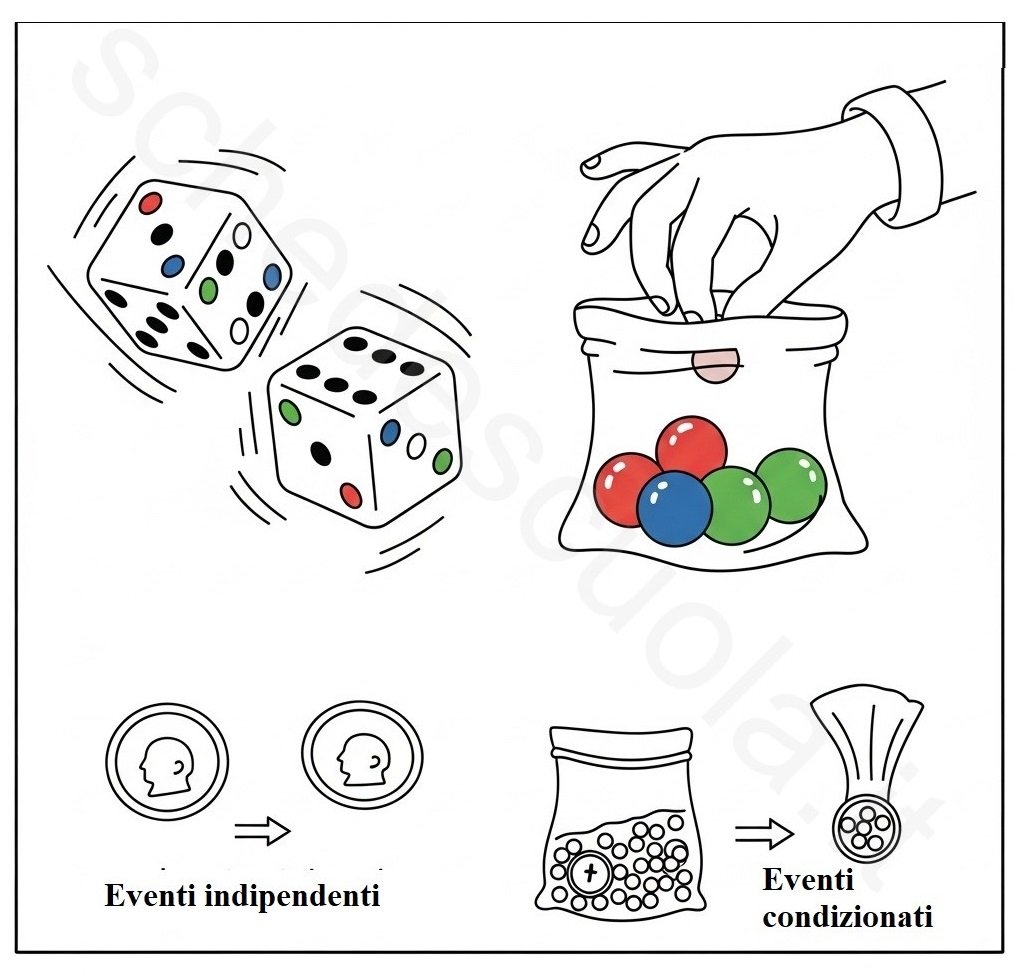
Ci sono tre tipi di eventi speciali da conoscere:

Eventi dipendenti: Due eventi sono dipendenti se il verificarsi di uno influenza direttamente la probabilità che si verifichi l’altro.
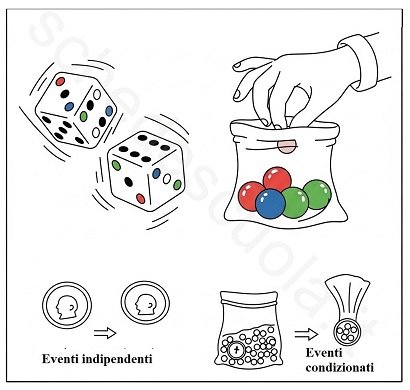
Eventi Indipendenti: Pensate a quando lanciate una moneta due volte. Il risultato del primo lancio (testa o croce) non cambia il risultato del secondo lancio. Sono due eventi che non si influenzano a vicenda. Ogni lancio è “indipendente” dall’altro!
Probabilità Condizionata: Qui le cose si fanno più interessanti! Immaginate di avere un sacchetto pieno di caramelle di diversi colori. Se ne prendete una senza guardare e la mangiate, la probabilità di pescare un certo colore la seconda volta cambierà, perché una caramella è sparita! La probabilità del secondo evento è “condizionata” dal risultato del primo.

Probabilità Condizionata: Quando un Evento “Parla” all’Altro

Immagina la probabilità condizionata come una conversazione tra eventi. È la probabilità che succeda qualcosa (Evento A) sapendo già che qualcos’altro (Evento B) è già successo. È come dire: “Qual è la probabilità che io prenda un bel voto in matematica, dato che ho studiato per due ore?”. Studiare (Evento B) influenza la probabilità di prendere un bel voto (Evento A).

Si indica con (A∣B), che si legge “probabilità di A dato B”.

Esempio classico: Hai un sacchetto con 5 caramelle rosse e 5 caramelle blu (totale 10).

Probabilità di pescare una caramella rossa la prima volta? (Rossa 1a volta)=5/10=1/2.
Ora, se hai già pescato una caramella rossa (e non l’hai rimessa nel sacchetto), quante caramelle rosse e quante totali ti sono rimaste? Ti restano 4 rosse e 5 blu, per un totale di 9.
Qual è la probabilità di pescare un’altra caramella rossa la seconda volta, dato che la prima era rossa? (Rossa 2a volta | Rossa 1a volta)=4/9. Vedi? La probabilità è cambiata perché il primo evento ha modificato la situazione.

Eventi Indipendenti: Ognuno per Sé!

Due eventi sono indipendenti se il verificarsi di uno non cambia in alcun modo la probabilità che si verifichi l’altro. Non si “parlano” e non si influenzano.

Esempio: Lanci una moneta e poi lanci un dado.

Il risultato del lancio della moneta (testa o croce) non influenzerà mai il numero che uscirà dal dado.
La probabilità di ottenere “testa” con la moneta è .
La probabilità di ottenere “3” con il dado è . Questi due eventi sono completamente scollegati. Per calcolare la probabilità che accadano entrambi, moltiplichi le loro singole probabilità: (Testa e 3)=P(Testa)×P(3)=1/2×1/6=1/12.

Eventi Dipendenti: Un Effetto Domino domino effect

Due eventi sono dipendenti se il verificarsi di uno influenza direttamente la probabilità che si verifichi l’altro. Sono come due amici che si influenzano a vicenda. L’esempio della caramella dal sacchetto di prima è perfetto per questo!

Esempio (lo stesso della probabilità condizionata, perché sono concetti strettamente collegati!): Hai lo stesso sacchetto con 5 caramelle rosse e 5 blu.

Evento 1: Peschi una caramella rossa. La probabilità è .
Evento 2: Peschi una seconda caramella rossa senza rimettere la prima. La probabilità del secondo evento è ora . Perché? Perché l’esito del primo evento (aver rimosso una caramella rossa) ha modificato il numero totale di caramelle e il numero di caramelle rosse rimaste. Il secondo evento è dipendente dal primo.

Per riassumere:

Indipendenti: Nessuna connessione, una cosa non cambia le probabilità dell’altra. Pensa a due diverse partite di calcio giocate contemporaneamente.
Dipendenti: Una cosa cambia le probabilità dell’altra. Pensa a pescare carte da un mazzo senza rimetterle dentro.
Probabilità Condizionata: È il modo in cui calcoliamo la probabilità di un evento quando sappiamo già che un evento dipendente si è verificato.

Facciamo un esempio: Lancio di due dadi!

Proviamo con i dadi! Se lanciate due dadi, quante combinazioni diverse potete ottenere? Ogni dado ha 6 facce, quindi ×6=36 combinazioni possibili in totale.

Qual è la probabilità di ottenere un totale di 7 con due dadi?

Dobbiamo trovare tutte le coppie di numeri che, sommate, danno 7:

(1 e 6)
(2 e 5)
(3 e 4)
(4 e 3)
(5 e 2)
(6 e 1)

Ci sono 6 combinazioni possibili per ottenere un 7.

Quindi, la probabilità di ottenere un 7 è il numero di combinazioni favorevoli diviso il numero totale di combinazioni: Probabilità = 6 : 36, che si semplifica a 1 su 6!

Questo significa che, in media, ogni 6 lanci, uno darà un 7.

Curiosità sul Calcolo delle Probabilità!

Da dove viene? La teoria della probabilità è nata nel XVII secolo per studiare i giochi d’azzardo! I matematici cercavano di capire come aumentare le loro possibilità di vincita.
Dove la usiamo oggi? Non solo nei giochi! La probabilità è usata in tantissimi campi: per prevedere il meteo, per capire la diffusione delle malattie, per progettare auto più sicure e persino per creare gli effetti speciali nei film!
Il paradosso del compleanno: Questa è divertente! Se in una stanza ci sono solo 23 persone, c’è più del 50% di probabilità che due di loro festeggino il compleanno nello stesso giorno. Sembra strano, vero? Ma è vero!

Ora prova tu!

Disegna un sacchetto con 3 palline rosse, 2 blu e 1 verde.

Qual è la probabilità di pescare una pallina blu al primo tentativo?

Numero totale di palline nel sacchetto: ______
Numero di palline blu: ______
Probabilità di pescare una pallina blu: ______ su ______

Gioco finale: I Dadi Fortunati!

Disegna due dadi qui sotto. Quante combinazioni possibili ci sono per ottenere un totale di 8?

(Elenca le combinazioni: es. (2,6), …) ___________________________________________
Numero totale di combinazioni per un 8: ______
Calcola la probabilità di ottenere un 8 (ricorda, il totale delle combinazioni è 36!):Probabilità = ______ su ______

Sei pronto a svelare altri misteri del caso? Continua a esplorare il mondo della probabilità!

Scopri https://www.amazon.it/dp/B0FH685KZ2

Leggi https://rimediomeopatici.com/fame-nervosa/